DP

背包问题

背包九讲问题-dd大牛的《背包九讲》

0-1背包问题

有n 个物品，它们有各自的体积/重量和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？

每件物品只有一个

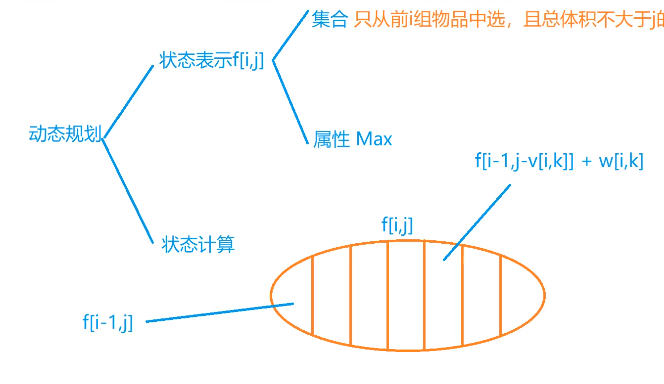
思路

二维（朴素）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1;i <= n ;i++){
        for(int j = 0;j <= m;j++){
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j],f[i - 1][j - v[i]]+ w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

一维优化（滚动数组）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1;i <= n ;i++){
        for(int j = m;j >=v[i];j--){//j从0-v[i-1]没有意义，逆序
            f[j] = max(f[j],f[j - v[i]]+ w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

极好的题解

完全背包问题

有n 个物品，它们有各自的体积/重量和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？

每件物品有无限个

思路

朴素

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1;i <= n ;i++){
        for(int j = 0;j <= m;j++){
            for(int k = 0;k*v[i] <= j;k++){
                 f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

优化(简化内部关系)

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N][N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1;i <= n ;i++){
        for(int j = 0;j <= m;j++){
            f[i][j] = f[i-1][j];
            if(j-v[i]>=0)
                f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

一维优化

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i];
    
    for(int i = 1 ; i<=n ;i++)
        for(int j = 0;j <= m;j++){//从小到大循环
            if(j-v[i]>=0)
                f[j]=max(f[j],f[j-v[i]]+w[i]);
            //当前不放的状态和放了的状态比较
        }
        
    cout << f[m] << endl;
    return 0;
}

多重背包问题

有n 个物品，它们有各自的体积/重量和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？

每件物品有$s_i$个

思路

朴素

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;

int n,m;
int v[N]={0},w[N]={0};
int f[N][N],s[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n; i++) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1;i <= n ;i++){
        for(int j = 0;j <= m;j++){
            for(int k = 0;k*v[i] <= j && k <= s[i];k++){
                 f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

优化（二进制优化、0-1背包）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000,M=2010;

int n,m;
int v[N]={0},w[N]={0};
int f[M];

int main()
{
    cin >> n >> m;
    int cnt=0;
    
    for(int i = 1;i <= n; i++) {
        int a,b,s;
        cin >> a >> b >> s;
        int k=1;
        while(k<=s){
            cnt++;
            v[cnt] = a*k;
            w[cnt] = b*k;
            s-=k;
            k *= 2;
        }
        
        if(s > 0) {
            cnt++;
            v[cnt] = a*s;
            w[cnt] = b*s;
        }
    }
    
    n = cnt;
    
    for(int i = 1;i <= n ;i++){
        for(int j = m;j >= v[i];j--){
            f[j] = max(f[j],f[j-v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

分组背包问题

有 N 组物品和一个容量是 V 的背包。每组物品有若干个，同一组内的物品最多只能选一个。每件物品的体积是 $v_{ij}$，价值是 $w_{ij}$，其中 i 是组号，j 是组内编号。求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

思路

优化（0-1背包）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 110;

int n,m;
int v[N][N],w[N][N],s[N];
int f[N];

int main()
{
    cin >> n >> m;
    
    for(int i = 1;i <= n;i++){
        cin >> s[i];
        for(int j = 0;j < s[i];j++){//注意
            cin >> v[i][j] >> w[i][j];
        }
    }
    
    for (int i = 1; i <= n; ++i) // 遍历每一组物品  
    for (int j = m; j >= 0; --j) // 遍历背包容量从m到0  
        for (int k = 0; k < s[i]; ++k) // 遍历第i组中的每个物品  
            if (v[i][k] <= j) // 如果当前物品可以放入背包中  
                // 更新背包的最大价值，考虑放入当前物品或不放入的情况  
                f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);  
                
    cout << f[m] << endl;
    return 0;
}

线性DP